หมวดหมู่ของบทความนี้จะพูดถึงsin 50 หากคุณต้องการเรียนรู้เกี่ยวกับsin 50มาเรียนรู้เกี่ยวกับหัวข้อsin 50กับpopasia.netในโพสต์sin(10°)sin(30°)sin(50°)sin(70°) = ? No calculator!นี้.
สารบัญ
เนื้อหาที่มีรายละเอียดมากที่สุดเกี่ยวกับsin 50ในsin(10°)sin(30°)sin(50°)sin(70°) = ? No calculator!
ที่เว็บไซต์PopAsiaคุณสามารถอัปเดตความรู้อื่นนอกเหนือจากsin 50ได้รับความรู้ที่มีคุณค่ามากขึ้นสำหรับคุณ ที่เว็บไซต์Pop Asia เราแจ้งให้คุณทราบด้วยเนื้อหาใหม่และถูกต้องทุกวัน, ด้วยความหวังว่าจะให้ข้อมูลรายละเอียดมากที่สุดสำหรับคุณ ช่วยให้คุณติดตามข่าวสารทางอินเทอร์เน็ตได้รวดเร็วที่สุดcách.
แชร์ที่เกี่ยวข้องกับหัวข้อ sin 50
ประเมินค่าบาป (10°)บาป(30°)บาป(50°)บาป(70°) ไม่ต้องใช้เครื่องคิดเลขแต่ใช้เอกลักษณ์ของฟังก์ชันร่วมและเอกลักษณ์แบบสองมุม สมัครรับวิดีโอคณิตศาสตร์เพิ่มเติมเพื่อความสนุก 👉 🛍 เลือกซื้อเสื้อยืดคณิตศาสตร์และเสื้อฮู้ด: (ลด 10% เมื่อใช้โค้ด “WELCOME10”) blackpenredpen
รูปภาพบางส่วนที่เกี่ยวข้องกับหมวดหมู่เกี่ยวกับsin 50
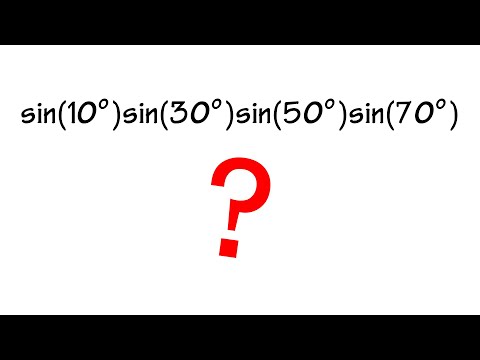
นอกจากการหาข้อมูลเกี่ยวกับบทความนี้ sin(10°)sin(30°)sin(50°)sin(70°) = ? No calculator! สามารถรับชมและอ่านเนื้อหาเพิ่มเติมได้ที่ด้านล่าง
คำหลักบางคำที่เกี่ยวข้องกับsin 50
#sin10sin30sin50sin70 #calculator.
sin(10)sin(30)sin(50)sin(70),fun trig problems,challenging math problem,using co-function identity and double angle identity,Evaluate sin(10°)sin(30°)sin(50°)sin(70°),co-function identity,double angle identity,math for fun,let’s do some math for fun,sine of 10 degrees times sine of 30 degrees times sine of 50 degrees times sine of 70 degree,no calculator,math competition,classic math competition.
sin(10°)sin(30°)sin(50°)sin(70°) = ? No calculator!.
sin 50.
หวังว่าคุณค่าที่เรามอบให้จะเป็นประโยชน์กับคุณ ขอบคุณมากสำหรับการอ่านsin 50ข่าวของเรา

"I'm not gonna use a calculator otherwise you defeat the whole purpose of doing math"
I will forever tell myself this
Math is fun actually
I'm from India love you brother
Thank you for solving using basics of trigonometry.. rather than using stuff randomly to multiply or divide on both sides blah blah… My math teacher used to do that.. and I've never understood why she multiplied with a particular number on both sides. From where did that number come in the first place.. i used to have all these questions which nobody gave answers to… Now I'm brushing my basics and i feel like I'm enjoying math.
Hermoso. De que país sos?
Sin 8.69 ???
Rd sharma class 11 ch 7 ex 1
This came in my 11th exam
Is there an formula that would give me cos(pi/100) or cos(e), etc?
You're one of the people who made me feel like enjoying this particular problem. Before seeing this video, I only thought how to solve it for my upcoming examination.
Thank you so so much. You are a brilliant person!
So glad to have found this channel.
y one half reason
That is really cool
Excellent trick
Thank you man
It is cool
Thanks
Really an exceptional way of doing a problem
After re-writing in terms of cosine
Okay, let's see…I already know that cos(20)cos(40)cos(80) is 1/8 (yes, I came from that other video), and now multiplying with cos(60) gives me 1/16.
That is too easy question
Well, I just happen to have watched his other vid on sine of 10, 50 and -70 degrees. The answer is obvious from there. 1/16 or 0.0625
Maybe find an algebraic expression for sin 18°, cos 18°, and tan 18°.
How to find cotπ/24 value
And yet again such an elegant proof.
I did it in a more effortful way but I'm still proud to have solved it on my own (apart from looking up some identities I don't know by heart, like sin(x±y)=sin(x)cos(y)±cos(x)sin(y) and sin(3x)=3sin(x)-4sin³(x)). My way was this:
First look at the last two terms whose angles can be expressed in terms of two other angles:
sin(50°)sin(70°) = sin(60°–10°)sin(60°+10°)
Using the trigonometric identity:
sin(x±y) = sin(x)cos(y) ± cos(x)sin(y)
For x=60° and y=10° we get:
sin(60°±10°) = sin(60°)cos(10°) ± cos(60°)sin(10°) = √(3)/2 cos(10°) ± 1/2 sin(10°) [= a ± b]
Therefore:
sin(50°)sin(70°) = [(a–b)(a+b) = a² – b² =] 3/4 cos²(10°) – 1/4 sin²(10°) = 3/4 – sin²(10°)
Now the whole product:
sin(10°)sin(30°)sin(50°)sin(70°)
= sin(10°)*1/2*(3/4–sin²(10°))
= 1/8*(3sin(10°)–4sin³(10°))[trig identity sin(3x)=3sin(x)-4sin³(x)]
= 1/8*sin(30°)
= 1/16
speak slowly pls
806 likes 0 dislike
I am definitely using this as a thought problem for my Trig students
superb
Good one chappie
can you make dotted line?
Can you make a video on beauty of drawing tricky graphs?
Cool idea! Cute result!
It definitely is very amazing that the product of four trig functions, even though three don't seem to have any obvious rational or radical values, is rational. I found this video very interesting; it has opened me up to a new trig idea that I have never thought of before. I like algebra and am sure I will like calculus when I do it next year, so I really like these algebra and calculus videos that you create. Keep up the good work!
Can u solve ln(x)=x?
Lol peyam starts on the white board, bprp goes straight for the chalk
Maybe you could try yellow chalk instead of the red one next video. Yellow chalks are more clear and better for pointing out the key by my learning experience.
sin10º sin30º sin50º sin70º = 1/16 Use sinA sinB = ½(cos(B–A) – cos(B+A))
Then it's just a matter of which of the 3 possible double-pairings to use, for those 4 sine factors. E.g.,
sin10º sin70º = ½(cos60º – cos80º) = ½(sin30º – sin10º) = ¼(1 – 2sin10º)
sin30º sin50º = ½(cos20º – cos80º) = ½(1 – 2sin²10º – sin10º)
Now let s = sin10º . . . Then:
½ = sin30º = sin(3·10º) = 3s – 4s³ . . . and:
sin10º sin30º sin50º sin70º = ⅛(1 – 2s)(1 – s – 2s²) = ⅛(1 – 3s + 4s³) = ⅛(1 – ½) = 1/16
Post-view:
I like your method better.
So is this the "other way" you mentioned at the end?
Fred
What made you decide to use chalk? Also, why not use the half-angle identity? It has no squares.
Clever
Thanks friend for all math videos – finished all math/calculus exams !!! Now math is more fun when it's not just about scoring haha
Please can you make a video without that black ball. It is making me scared. I am afraid of Darth Vader!
A M U S E M E N T
Btw, you can easily find the quintuple angle formula for sin, or for any a (a is an integer) of sin(ax)
I just came acrossa min/max geometry problem for example:
find the biggest possible are of a cylinder inside a cone, altho it's an easy one you can do a fun one, they are just about a one for a good long but not boring video, and they are just fun to know 🙂