ข้อมูลของบทความนี้จะเกี่ยวกับcos1 หากคุณกำลังเรียนรู้เกี่ยวกับcos1มาถอดรหัสหัวข้อcos1กับPop Asiaในโพสต์cos(1) + … + cos(n)นี้.
สารบัญ
ข้อมูลทั่วไปเกี่ยวกับcos1ในcos(1) + … + cos(n)โดยละเอียด
ที่เว็บไซต์popasia.netคุณสามารถอัปเดตข้อมูลอื่น ๆ นอกเหนือจากcos1เพื่อรับความรู้เพิ่มคุณค่าให้กับคุณ ในหน้าPopAsia เราแจ้งให้คุณทราบด้วยเนื้อหาใหม่และถูกต้องทุกวัน, ด้วยความหวังว่าจะให้บริการข่าวสารที่แม่นยำที่สุดแก่ผู้ใช้งาน ช่วยให้คุณได้รับข้อมูลทางอินเทอร์เน็ตโดยเร็วที่สุด.
หุ้นที่เกี่ยวข้องกับหมวดหมู่cos1
ในวิดีโอนี้ ฉันคำนวณผลรวมของ cos(1) + … + cos(n) เช่นเดียวกับ sin(1) + … + sin(n) โดยการสำรวจโลกที่ซับซ้อนอย่างรวดเร็ว นี่เป็นหนึ่งในกรณีทางคณิตศาสตร์ที่คุณเปลี่ยนมันให้เป็นปัญหาที่ยากในการแก้ปัญหาของคุณ! สนุก!
ภาพถ่ายบางส่วนที่เกี่ยวข้องกับหมวดหมู่ของcos1
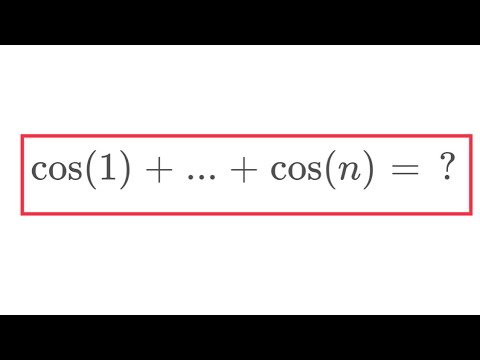
นอกจากการเรียนรู้เนื้อหาของบทความ cos(1) + … + cos(n) นี้แล้ว สามารถรับชมและอ่านเนื้อหาเพิ่มเติมได้ที่ด้านล่าง
คำหลักบางคำที่เกี่ยวข้องกับcos1
#cos1 #cosn.
cos(1) + … + cos(n),cos(1) + cos(2) + … + cos(n),sin(1) + … + sin(n),eix,complex,complex numbers,calculus,geometric series,interesting sum,math.
cos(1) + … + cos(n).
cos1.
หวังว่าข้อมูลบางส่วนที่เราให้ไว้จะเป็นประโยชน์กับคุณ ขอขอบคุณที่อ่านcos1ข่าวของเรา

great video thank you soo much ^^
I love your energy. Great video!
This is so cool!!!
Ah, the Dirichlet kernel. Fun fact: If you sum all the odd or even up to n of Chebyshev polynomials of the first kind T_n(x), you get the nth Chebyshev polynomials of the second kind U_n(x), which happens to be the polynomial expression of the Dirichlet kernel when composed with cos(x).
Conversely you, work backwards and get T_n (x) from U_n(x) by taking the difference of two U polynomials since all the cumulative sums cancel except for the last term. But another interesting thing is that U_n-1(x)*n is the derivative of T_n(x),
So taking a finite sum in one domain gives you a derivative in the other domain, and taking a finite difference gives you an antiderivative in the other domain. I always thought that inverse relationship was interesting, Sort of like fourier duality but with polynomials.
he teaches with light smile.it makes my mind consolation
Wowww….
I studied this in GSEB textbook of this formula but the proof was given by PMI but I needed real proof.
むぅーーーん なるほど
これがスっとできちゃうには、sinやeに相当馴染まないといけないねえ!
woo
Where did the isin(x) terms go from e^i
Woww amazing how complexe world can solve a real problem !!!!!!!!!!!!!!!!!!!!!!!!!!!
Love this video!
Nice.
Depends on n being degree or radian
I thought the geometric series was (1-r^(m+1))/(1-r) ?
Not only that, if u divide those sums u precisely get tan((n+1)/2) . How cool is that!!
Wow im so impressed
Can give other solution without complex number?
I'm not good at infinite series but
Can someone explain why it isn't just cos (1)
I mean
If we have infinitely terms that go from one to infinity
We could stipulate that we basically have an infinite amount of circles with an extra cos(1) thrown in…?
I just want you to know you are a savior. tons of love from Iran.
Be kar vedio
oh yes, when we started to learn trigonometric functions on high school this was a challenge. Here is how i solved it at the time :
obs: sin(a+b)+sin(a-b)=2sin(a)cos(b)
and cos(a+b)+cos(a-b)=2cos(a)cos(b)
f(x,n)=sin(x)+sin(2x)+sin(3x)+…+sin(nx)
2 f(x,n) cos(x)=(sin(2x)+sin(3x)+sin(4x)+…+sin((n+1)x))+(sin(0x)+sin(x)+sin(2x)+…+sin((n-1)x))
2 f(x,n) cos(x)=(f(x,n)–sin(x)+sin((n+1)x))+(f(x,n)-sin(nx)+sin(0))
2 f(x,n) (1–cos(x))=sin(x)+sin(nx)–sin((n+1)x)
g(x,n)=cos(x)+cos(2x)+cos(3x)+…+cos(nx)
2 g(x,n) cos(x)= (cos(2x)+cos(3x)+cos(4x)+…+cos((n+1)x))+(cos(0x)+cos(x)+cos(2x)+…+cos((n-1)x))
2 g(x,n) cos(x)=(g(x,n)–cos(x)+cos((n+1)x))+(g(x,n)+cos(0)-cos(nx))
2 g(x,n) (1–cos(x))=cos(x)–1+cos(nx)–cos((n+1)x)
Nothing much different from the other comments i think . I find it pleasing to plot this function.
edit: i remember spending so much time doing some convoluted calculations and etc.
Good stuff. Needs more lighting on the whiteboard. Always following your lecture.
What happens if we use the definition of dirichilet kernel directly?…maybe the answer will come in a different form and we won't get the bonus formula for sin
Did you kill two birds with one stone?
I had an interesting trick for this aswell only for sum of sin(n). I did it using telescoping sums. Not as extravagant as using complex numbers though sadly.
This series is actually very useful for phased array antennae.
Nice! If you don't love complex numbers, you don't love math 🙂
Nice proof
I used trigonometric identities to proof this when i was at highschool but that was messy. This proof much more elegant
They are complex and complicated numbers
that was totally enjoyable,thank you very much DR Peyam 🙂
I'm from bihar and also knew these trick
This could be hard to made for tan(n×x) if some cases the tan(j×x) (0<j<=n) gives infinity.
Euler formular is…. just fantastic.
Omg, could you use this thing to calculate the integral of cos(x)? Or sin(x). Off course this wouldn't be usefull as a proof for the derivatives of sinx because it would be circular. Because Eulers identity uses the derivatives and integral of sinx and cosx already.
Use the horse shoe
Uau !
Jobb kéz érted? Csak próbáld ki ok! Tudom nem fog menni! Tanuld meg! Csak egy kérdés! Mit csinálsz ha medvével találkozol? Nos:? :
Why didn't you use the cos and sin sum of angles formulas?( in this case sum of n/2 and 1/2) They may could be much easier to use in terms of tan and cot. I actually don't know, this is a question.
"COOOOOL"
By using brut force i got to:
[-1+cos(1)-cos(n+1)+cos(n)]/(2-2cos(1))
But your answer is much more beauty.
Can you do a video, showing that the series diverges when it goes to infinity and why
As soon as I saw that, I knew the right way was Euler 🙂
sir you are my inspiration
Deux pour le prix d'un .
Since the defined domain for the geometric series is |z| < 1, is it really fine to use the geometric series for e^ix, which has a modulus of precisely 1?
i graphed the sum and it seemed to align suspiciosly well with sin(x)+1/2